Note To Mitscherlich's Law – An Alternative More General Hypothesis
H. Schneeberger
Institute of Statistics, University of Erlangen-Nürnberg, Germany
2014, 25th September
Abstract
A formula is presented, which describes not only the ascending part of the fertilizer-yield curve (such as Mitscherlich's Law does), but also the descending part.
Introduction
Mitscherlich introduced his hypothesis for the ferilizer-yield relationship as Law of decreasing growth of yield with increasing quantity of fertilizer ("Gesetz vom abnehmenden Ertragszuwachs"), mathematically by the differential equation
 (1)
(1)
x = quantity of fertilizer
y = yield (data values); ŷ = hypothesis
Formula (1) means, that dŷ/dx is a negative linear function of ŷ with factor of proportionality b; a is the asymptotic value of the yield. So (1) is a monotonic function and can only be valid for the increasing part of the fertilizer-yield curve.
The solution of (1) is (see [3] and figure 1a)
(M1) ŷ = a(1-e-bz) = a(1-e-b(x-d)) (2)
The 3 parameters a, b and d must be estimated with the data. This is done with the method of Least Squares of Gauss, using the method of Nelder & Mead [2] for minimization.
The author generalized hypothesis (1) for the decreasing part of the fertilizer-yield curve by the hypothesis, that this decreasing process is an inverse increasing Mitscherlich process, i.e. with u = -x+d2
ŷ2 = a2 (1-e-b2u) = a2 (1-e-b2(d2-x)) (3)
and because of a2 = a (process (1) turns into process (3))
(M2)ŷ2 = a - ae -b2d2 eb2x (4)
(see [5] and figure 1b). For estimating process (M1) and process (M2) 5 parameters must be estimated with the the method of Gauss and the iterative method of Nelder and Mead.
Alternative Definition of the Mitscherlich's Process (M1)
The processp(z) = p1(z) * p2(z) = a(ebz-1) * e-bz (5)
is the product of two exponential processes: p1(z) is an exponential growing process with p1(z)= 0 for z=0; p2(z) is an exponential dying process with p2(z) → 0 for z → ∞. p(z) is identical with Mitscherlich's ascending process (2): p(z) = a(1 - e-bz).

Comments
1. Processes, defined by formula (1) or (5), are processes with saturation (value a). Well-known processes of this sort are Mendel's Law in genetics, or the charging of an auto-battery. The fertilizer-yield process isn't a saturation process! The yield y goes to zero for great values of fertilizer x. Mitscherlich himself stated this in drastical manner ([1], p. 172): In a concentrated saline solution no plant can grow ("in konzentrierter Salzlösung kann keine Pflanze gedeihen").
2. Processes as product of other processes are well-known in physics. So Wien's law of radiation is of the form p(z) = az3 * e-bz and Planck's famous formula of radiation is of the form
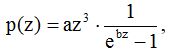
where p(z) is the intensity of radiation, and z the frequency.
Alternative Hypothesis for the Increasing and Decreasing Process
This most simple hypothesis
(S)ŷ = az * e-bz = a(x-d) * e -b(x-d) (6)
is the product of
a) a linear growing process with ŷ1 = az = a(x-d) with ŷ = 0 for z=0 or x=d, and
b) an exponential dying process ŷ2 = e-bz = e -b(x-d)
The linear growing process is superposed by an exponential dying process. The 3 parameters a, b and d are again estimated with Gauss and Nelder & Mead.
Application
As example I use the data given in [5], which are repeated here. For convenience the x- and y-values there are multiplied by 10-2, the y-values here are the ȳ-values of [5].
Increasing part of the fertilizer-yield curve
| x | 0 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
| y | 0.6312 | 0.8672 | 0.9715 | 1.0380 | 1.0612 | 1.0697 | 1.0647 |
Decreasing part of the fertilizer-yield curve
| x | 1.8 | 2 | 2 | 2.2 | 2.4 | 2.6 | 3 |
| y | 1.0182 | 1.0285 | 1.0790 | 1.0505 | 0.9602 | 0.8747 | 0.8515 |
Mitscherlich's curve (M1) for the increasing part of the fertilizer-yield curve then becomes
(M1)ŷM1 = 1.1154 (1-e -1.98(x+0.416)) (7)
and for the decreasing part of the curve (M2) we get
(M2)ŷM2 = 1.1154 - 0.00788 * e 1.197x) (8)
In figure 2 the data-points are marked by stars, (M1) and (M2) are broken lines. The alternative hypothesis (S) yields (with Gauss and Nelder & Mead)
(S)ŷS = 1.557 (x + 0.5323) * e -0.5301 (x + 0.5323) (9)
see also figure 2. One can see, that the increasing part of the fertilizer-yield curve as well as the decreasing part are very well declared by one formula!

From the point of correspondence of data and hypothesis one not could state (with these data), that hypotheses (M) or hypothesis (S) are the "better" ones. To make a general decision, further experiments, especially with greater values of x (i.e. for overfertilization) would be necessary. It is shown in figure 2, that for greater values of x the ŷ-curves for both hypotheses are far diverging. Secondly and above all: The variance of the data-points should be reduced. The present data were obtained by field-experiments. For basic research like this pot-experiments in green houses would be advisable.
In any case Mitscherlich's hypothesis (M1) and hypothesis (M2) will remain a very good approximation to the data in the most interesting part of the fertilizer-yield curve; with all the consequences, drawn from this formulae (see e.g.[4]).
Generalization
In analogy to papers [6] and [7] the yield in dependence on two fertilizers will be
ŷ(x1, x2) = a * z1e -b1z1 * z2e -b2z2 with z1 = x1 - d1; z2 = x2 - d2 (10)
The parameters a, b1, b2, d1, d2 must be estimated from the data in the well-known way.
References
[1] Mitscherlich, E.A. (1954). Bodenkunde für Landwirte, Forstwirte und Gärtner, 7. Auflage, Paul Parey Verlag
[2] Nelder,J.R. and Mead,R. (1965). A Simplex Method for function minimization. The Computer Journal 7, 303-313
[3] Schneeberger, H. (2009). Mitscherlich's Law. Sum of two exponential Processes. Conclusions. Internet: www.soil-statistic.de, paper 1
[4] Schneeberger, (2010). Mitscherlich's Law: A Supplement. Internet: www.soil-statistic.de, paper 2
[5] Schneeberger,H. (2009). Overfertilization: An Inverse Mitscherlich Process. Internet: www.soil-statistic.de, paper 3a
[6] Schneeberger,H. (2010). Mitscherlich's Law: Generalization with several fertilizers. Internet: www.soil-statistic.de, paper 4
[7] Schneeberger,H. (2010). Mitscherlich's Law: Generalization with several fertilizers and overfertilization. Internet: www.soil-statistic.de, paper 5
SupplementJune 2015
This is a reply to paper [8], as there are not only diminishing returns, but also growing returns. The consequence is a further restriction of Mitscherlich's Law.
1. By chance I found in the internet the paper [8] with title "Growth response curves – the law of diminishing returns". There a figure gives the corn-yield on a very phosphate-deficient soil, result of an experiment done by the Department of Agronomy and Soil Science, College of Tropical Agriculture, University of Hawai. Phoshate was added ... Figure 3 is a copy, reduced in size.

Figure 3: Growth response curves - "The Law of diminishing returns"
The graph is very illustrative, as along the (fertilizer,yield)-curve corn-plants with growing height are lined up. Unfortunately no data are given, so that no own calculations could be made. But the curve itself is very instructive. It has a point of inflection! This surely comes from the "very phosphate-deficient soil". But the solution of Mitscherlich's differential equation
cited in paper [8], namely
ŷ' = b(a - y)
ŷ = a(1 - e-b(x - d))
(a = yMax; ŷ(x = d) = 0), as given by B. Baule [9], has no point of inflection, as ŷ" ≠ 0 for 0 < y < a. Also the slogan of "diminishing return" is only right for x > xi, where xi stands for point of inflection. In figure 3 we have xi ≈ 300 > x0 = 0;. For x < xi we even have growing return! So only for x > xi we have diminishing return and only then it is justified to speak of the law of diminishing returns, as the author Fox in paper [8] erroneously does for all values of x > 0.
It is the natural way in natural sciences, that hypotheses or laws, which no longer comply with the experience, are replaced by new ones. The most-known example is the replacement of the geocentric by the heliocentric world-system by Kopernikus, Kepler, Galilei, Newton – after thousands of years. Another highly important problem was the exploration of the intensity of radiation in dependence on the frequency ν in the years 1890 - 1900 by the physicists Rayleigh & Jeans, Wien and Planck.
2. The second reason for this supplement is, that by chance the author was interested in the mathematical development of these physical formulae (see [10]).
A short abstract: It is well-known, that the exponential growth-function ex and its inverse e-x are of central importance in natural sciences. For the present application I introduced the "soft" exponential growth function  and its inverse
and its inverse 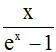 . Because of the name "soft" see figure 4.
. Because of the name "soft" see figure 4.

Figure 4: Exponetial functions
The three Laws: Intensity ŷ in dependence on the frequency x = ν (in standardized form) are

I tested with the data of the present paper the hypotheses (H), where z = x - d:
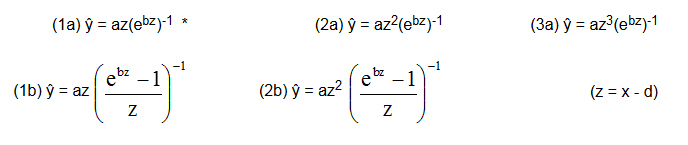
* in this paper carried out in detail (formula (6)).
Of course in a general investigation also higher powers of the form zp should be tested.
Figure 5 gives the results, table 1 the parameters a, b and d.

Figure 5: Curves (1a), (1b), (2a), (1b), (3a) and M1, M2
| a | b | d | |
|---|---|---|---|
| 1a | 1.5570 | 0.5301 | -0.5323 |
| 1b | 1.0490 | 0.7915 | -0.6172 |
| 2a | 1.2560 | 0.7902 | -1.1130 |
| 2b | 0.8081 | 1.0170 | -1.3210 |
| 3a | 0.7710 | 0.9831 | -1.6040 |
Table 1: Parameters a, b, d of hypotheses (H)
You see, that all hypotheses approximate the data very well. Beginning with the exponent p=2 of the term zp we have points of inflection.
For most soils (i.e. without great fertilizer-deficiency) we apparently have for the point of inflection xi < x0 = 0 and so this point doesn't become visible. If Fox' experiment with the result of a point of inflection is right, then formulas (H) are proposals for a generalized hypothesis. For then Mitscherlichs hypothesis "Law of diminishing return" is only a very good approximation for
x > xi and also gives no answer in the case of overfertilization
Before I came to Robert L. Fox' paper [8], I assumed, that the question, what hypothesis is the right one, must be solved by experiments with overfertilization, when the curves with different hypotheses are divergent. But this would be costly, as in the case of overfertilization more fertilizer brings smaller yield. I think, the better way is that of testing highly fertilizer-deficient soils. The right law can only be found with experiments according to the sentence in Planck's famous paper [11], p. 243: "Der Beweis kann in letzter Linie nur durch die Erfahrung geliefert warden' (the proof can – first of all – only be given by experience).
References
[8] Fox, Robert L. (1971). Internet: Growth Response-Curves – The "Law of Diminishing Returns".
[9] Baule, B. (1918). Zu Mitscherlichs Gesetz der physiologischen Beziehungen. Landw. Jahrbücher 51, 363-385.
[10] Schneeberger, H. (2015). Plancks Law: A Mathematical Deduction from the Law of Rayleigh-Jeans and the Law of Wien. www.plancks-law.de
[11] Planck, M. (1900). Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum. Verhandlungen der Dt. Phys. Ges. Berlin, Jhg.2, Nr.17, pp. 237-245.
Download this paper as PDF
Download this Paper in PDF format:
Note To Mitscherlich's Law – An Alternative More General Hypothesis [PDF, 270 kB]