• Impressum & Datenschutz
• Zurück zur Übersicht

Mitscherlich's Law: Sum of two exponential Processes
Conclusions

Hans Schneeberger
Institute of Statistics, University of Erlangen-Nürnberg, Germany
2009, 1^st July

Summary

It will be shown, that Mitscherlich's formula, the crop yield as function of the fertilizer, can be partitioned into two parts. One comes from the fertilizer in the soil, the other from the fertilizer, supplied from outside. As a consequence, the quantity of the fertilizer, which is extracted from the soil by the crop, can be computed. Correspondingly new fertilizing can be planned.

Introduction

One problem in fertilizing, on which many authors have worked, recently was reported on by Giebel et al. (2006): "Until now one may be able to derive a prognosis upon the spatial average of soil mineral-N content of a field. However, no approaches are available that would allow the estimation of the spatial distribution of plant-available N over an entire field within the same or a following year. Nevertheless, adequate representation of spatial N distribution within a field is important to site-specific and environmentally sustainable N fertilization". This result of spatial averages of soil mineral-N content of a field was obtained by Giebel et al. with samples of ground-drillings and a following analysis.

Another problem is the question, what part of the crop-yield comes from the plant-available fertilizer in the soil, and what part is caused by the given fertilizer. This problem is solved here in quite a different way without technical devices, only with analytical methods and the fact, that the Mitscherlich- process can be partitioned into two exponential processes. One of these processes is the so-called standardized Mitscherlich process, the other is an exponential dying process. From the quantity of lost fertilizer in the soil consequences for future fertilizing can be drawn.

The Law of Mitscherlich (1909) is an exponential growing process with horizontal asymptote. This sort of processes is widely known in natural sciences: In biology we find it as Mendel's law of genetics, in mechanics it is the generalization of Hooke's law (Schneeberger 2005): the first (linear) term of the Taylor-series of this generalization is Hooke's law; in electrical engineering charging of a battery follows this law, etc.

Mitscherlich first formulated the law in form of a differential equation:

(1)

where x is the quantity of fertilizer, y the crop-yield and (as usual in statistics) the hypothetical value of y; a is the maximum value of the yield (we exclude over-fertilization!) and b>0 is the most important exponential factor. Formula (1) means, that the growing of the crop is proportional to (a-). With boundary condition (x = 0) = c we have as solution of equation (1)

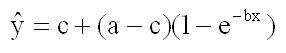(2)

The boundary condition (x = 0) = c means, that c is the crop-yield with only the plant-available fertilizer in the soil, with no supplementary fertilizer, i.e. x = 0. See the curve in figure 1.

Materials and Methods

For our analysis we use the results of an experiment with winter-wheat at the University of Technology München/Weihenstephan in 2002, given in table 1: For every of the r=15 values x_r of fertilizer, s=4 values of crop-yield y_rs are given. For clarity in the figures not the experimental points (x_r, y_rs) with the great variance of the y-values, but (x_r, ) are given as stars; see also the means in table 1.

Table 1: Yield y (winter-wheat in 100 kg/ha) for given fertilizer x (N in kg/ha)

r			1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
	s	xr	0	80	100	120	140	160	160	180	180	200	200	220	220	240	260
yrs
	1		40.8	73.8	79.6	84.5	97.7	82.9	96.2	102.6	102.8	96.4	103.5	98.6	102.7	102.2	108.1
	2		58.6	89.9	94.7	78.1	105.5	89.4	92.7	102.1	92.1	102.1	94.8	103.5	105.0	104.7	106.5
	3		62.7	76.4	84.4	78.2	80.4	109.0	97.6	103.4	104.7	102.0	104.8	93.7	104.0	97.7	110.0
	4		51.8	79.3	88.5	94.1	93.4	96.4	93.5	92.5	96.1	108.4	103.1	107.4	104.6	78.0	103.3
			53.475	79.850	86.800	83.725	94.250	94.425	95.000	100.150	98.925	102.225	101.550	100.800	104.075	95.650	106.975

The three parameters a,b,c of the Mitscherlich-curve (2) are estimated with the method of Least Squares of Gauss, i.e. a, b and c are solutions of the condition

(3)

This problem is solved iteratively with the non-linear Simplex-Method of Nelder and Mead (1965). The result is

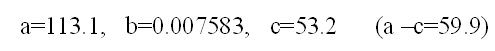(4)

(5)

It can easily be shown, that computation with the values of (instead of y) yields the same result.

The curve , plotted in figure 1, is extrapolated to negative values of x (dotted line). We get x = d = -83.8 as solution of (x) = 0. -d(>0) is the plant-available fertilizer in the soil, which gives the corresponding crop-yield =c=53.2, i.e. without fertilizing from outside. With this soil-immanent fertilizer -d we can write formula (2) also in the form of the Mitscherlich-Baule function (Baule 1918). See also Frank, Beattie and Embleton (1990):

(6)

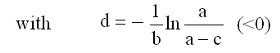(7)

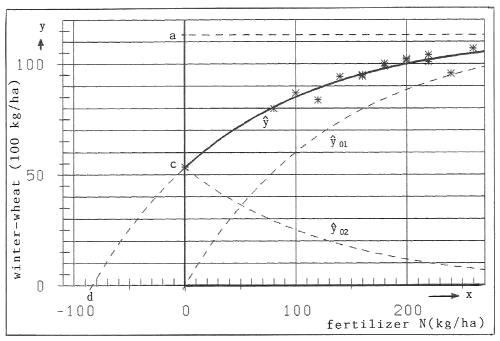
Figure 1. Partition of the Mitscherlich-curve into the two parts ₀₁ and ₀₂

The following theorem immediately results from formula (6):

Theorem: The general Mitscherlich-curve (x) of formula (6) with -d>0, or formula (2) with c>0, originates from the "standardized" Mitscherlich curve ₀₁(x)=a(1-e^-bx) with d=0 in formula (6) or c=0 in formula (2) by simply shifting the curve ₀₁(x) to the left for -d >0 units (of variable x). See figure 1.

For the strategy of fertilizing in the future, to avoid too much or too less fertilizing with the known consequences, it is important to state, that according to Liebig's Law we have for the total quantity q of plant-available fertilizer in the soil: q≥-d

Partition of Mitscherlich's Formula

We can write formula (2) in the form

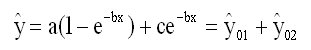(8)

The parts ₀₁ and ₀₂ are of specific importance:

a) 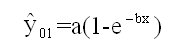(9)

is the standardized Mitscherlich process, beginning at the origin (x,)=(0,0), i.e. c=0. So this process is generated alone by the fertilizer, supplied from outside.

b) (10)

is a diminishing exponential process, starting from ₀₂(x=0)=c. So ₀₂(x) is the crop-yield, caused by the plant-available fertilizer in the soil alone. Note the remark to formula (2)!

Remark: Processes of the form (b) are the most important "dying processes" in natural sciences (e.g. radioactive decay), biology , medicine, economics, etc. Here one better would speak of an exhaustion process (of the fertilizer in the soil).

In figure 1 the curves ₀₁ and ₀₂ are plotted as dashed lines.

Results and discussion

If the quantity of fertilizer from outside is zero (i.e. x=0), we have ₀₁=0 and the crop is = ₀₂=c=53,2 (100 kg/ha of winter-wheat), which comes alone from the fertilizer in the soil -d=83.8 (kg/ha of N).

Now we assume, that for example a quantity of fertilizer x = x₀=100 kg/ha of N is given from outside. Then we get from formula (9) the quantity of crop ₀₁(x₀), which comes from the given x₀ and with formula (10) we get the quantity of crop ₀₂(x₀), which comes from the fertilizer in the soil. The total crop is (x₀)=₀₁(x₀)+₀₂(x₀) We get

₀₁(x₀)=60,1 |  ₀₂(x₀)=24,9 |  (x₀)=85,0

The problem now is: What quantity of fertilizer in the soil gives the crop ₀₂(x₀)? This is found with the auxiliary Mitscherlich process

(11)

which yields x=d₁=-32,8 as solution of ₁(x)=0. -d₁=32.8 (kg/ha) is the soil-immanent plant-available part of fertilizer, which, together with the fertilizer x₀=100 (kg/ha) from outside, yields the total crop (x₀)=85,0 (100 kg/ha). See figure 2.
Note: Equation (11) can also be written in the equivalent form:

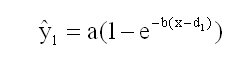(11a)

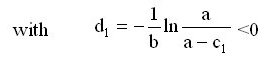
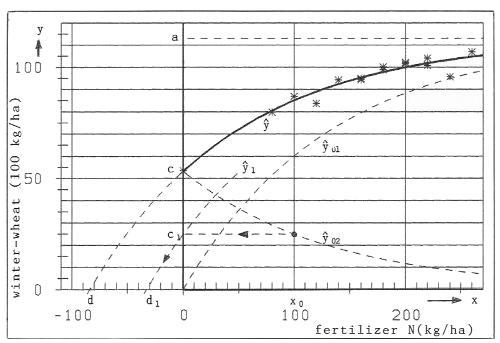
Figure 2: Example of fertilizing with x₀=100 kg/ha of N. Calculation of the quantity of fertilizer -d₁=32,8 kg/ha of N, supplied by the soil

A necessary supplement follows with Paper 2 (Paper 2: Mitcherlich's Law: A Supplement)

Acknowledgement

I have to thank Dr. Maidl of the University of Technology München (Weihenstephan)/Germany for providing me with the data, used in this article.

References