Mitscherlich's Law: Generalization with several Fertilizers and Overfertilization
H. Schneeberger
Institute of Statistics, University of Erlangen-Nürnberg, Germany
2010, 10th December
Abstract
Formulae and graphics for overfertilization with several fertilizers are given. It is shown, that a result, similar to Liebig's Law is valid: If by overfertilization with one fertilizer the crop-yield becomes zero, it remains zero, independent of the other fertilizers.
Introduction to Generalzed Overfertilization
Schneeberger (2009b, paper 3) presented a theory of overfertilization for one fertilizer x. The ascending part I of the fertilizer-yield curve is a Mitscherlich curve
![]() or
or ![]() according to Baule (1a)
according to Baule (1a)
and the descending part ![]() (1b)
(1b)
is an inverse Mitscherlich curve. See the symmetry of (1a) and (1b) in Baule's form! xA and xB are characterized by![]() 1(xA)=0 and
1(xA)=0 and ![]() 2(xB)=0.
2(xB)=0.
The parameters of formula (1a) and (1b) are calculated in paper 3 separately with the data of the ascending part I and with the data of the descending part II. The result led to the hypothesis: The parameters a1 and a2 are identical (=a), which is already realized in formulae (1a) and (1b). So one in future will make use of this hypothesis and estimate the five parameters c, a, b1, b2, xB of formulae (1a) and (1b) together by minimizing according to Gauss the combined function
![]() (2)
(2)
with the nonlinear Simplex-Method of Nelder and Mead (1965). z1i resp. z2i are the experimental values of the crop-yield with fertilizer x1i resp. x2i in I resp.II, ![]() 1i resp.
1i resp. ![]() 2i the corresponding hypothetical values. The result is in table 1, line 1.
2i the corresponding hypothetical values. The result is in table 1, line 1.
| c | a | b1 | b2 | xB | |
|---|---|---|---|---|---|
| line 1 | 62.75 | 112.6 | 0.0187 | 0.0122 | 418.9 |
| line 2 | 62.61 | 111.54 | 0.0198 | 0.01197 | 413.7 |
Line 2 repeats the results of paper 3. The good coincidence is a good sign for the hypothesis a1=a2=a. Figure 3 shows this result (cf. also figure 1 in paper 3).
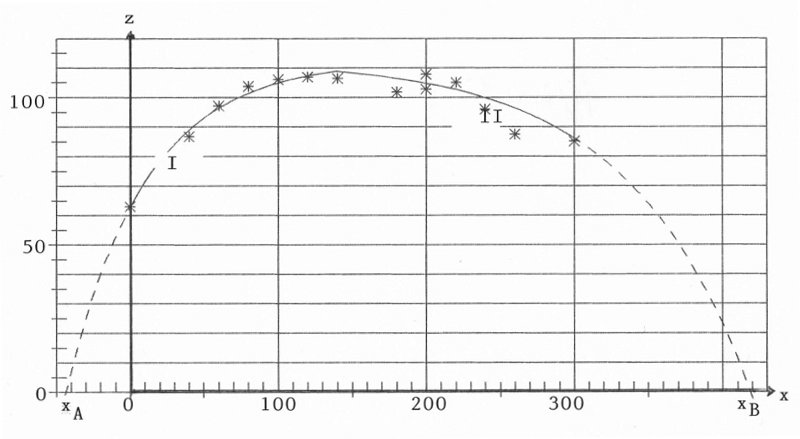
Figure 3: Crop-yield ![]() (x) with parameters of table 1, line 1
(x) with parameters of table 1, line 1
Overfertilization with two fertilizers
For illustration I confine to two fertilizers x and y; the further generalization is obvious. Schneeberger (2010 b, paper 4) gave for the case of no overfertilization the generalization of Mitscherlich's formula for two fertilizers x and y in the form
![]() (3)
(3)
see there the illustration of ![]() (x,y)=const. as contour-lines in figure 3a.
(x,y)=const. as contour-lines in figure 3a.
For the generalized case - two variables and overfertilization - formulae (2) and (3) are combined. For this we divide the (x,y)-plane in four sections (see figure 4):
- in section (1,1) there is overfertilization not for x, not for y
- in section (2,1) there is overfertilization for x, not for y
- in section (1,2) there is overfertilization not for x, for y
- in section (2,2) there is overfertilization for x, for y
For clearness I must modify the symbolic of formulae (1)
- for variable x
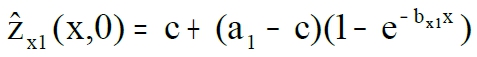 before overfertilization
before overfertilization - for variable x
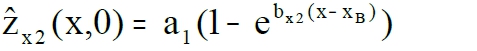 with overfertilization
with overfertilization - for variable y
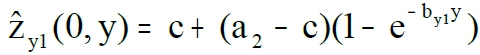 before overfertilization
before overfertilization - for variable y
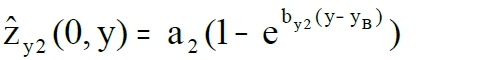 with overfertilization
with overfertilization
Then for estimation of the nine parameters c, a1, bx1, bx2, xB, a2, by1, by2, yB we minimize the function
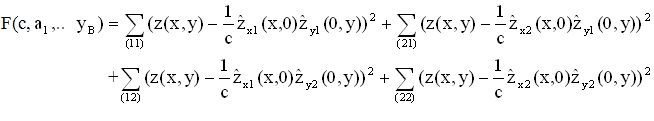 (4)
(4)
with the method of Nelder and Mead (1965). Summation is taken over the points of fertilizing (xi,yi) of the respective section (11), (21), (12), (22). With the resulting parameters we get the crop-yields ![]() (x,y)in the four sections:
(x,y)in the four sections:
![]() (5)
(5)
I regret it very much, that I have only the data of the example in paper 3, for overfertilization with one fertilizer, no data for two fertilizers. But I think that I can demonstrate the essential characteristics by choosing the parameters of variable x (those of table 1, line 1) also as parameters of variable y (a2=a1, by1=bx1, by2=bx2, yB=xB ) . As result we get the contour-lines of formula (5) in figure 4.
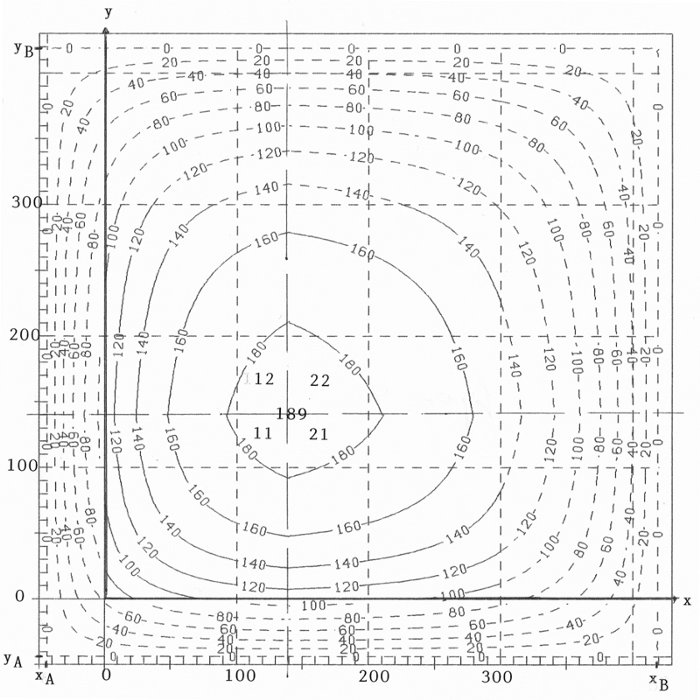
Figure 4: Contour-lines ![]() (x,y)=const.
(x,y)=const.
The symmetry to the bisector of the first quadrant of course comes from the symmetry of the parameters in x and y.
A conclusion, which can be drawn from figure 4: If overfertilization for one variable (=fertilizer) yields ![]() =0, then
=0, then ![]() remains zero, independent of the other fertilizers. This is an analogous statement to Liebig's Law, but now at the end of the fertilizing process.
remains zero, independent of the other fertilizers. This is an analogous statement to Liebig's Law, but now at the end of the fertilizing process.
Remark
It was assumed, that overfertilization ends with process (1b). The author tends to this hypothesis. In paper 3 another hypothesis with a part III of exponential dying was discussed. Then overfertilization would be generalized in analogous way. But the decision on the "right" hypothesis must be found with experiments.
References
Nelder, J.R. and Mead, R. (1965). A Simplex Method for function minimization. The Computer Journal 7, 303-313
Schneeberger, H. (2009b). Overfertilization: An Inverse Mitscherlich Process. Internet: http://www.soil-statistic.de, paper 3
Schneeberger, H. (2010b). Mitscherlich's Law: Generalization with several fertilizers. Internet: http://www.soil-statistic.de, paper 4
Download this paper as PDF
Download this Paper in PDF format:
Mitscherlich's Law: Generalization with several Fertilizers and Overfertilization [PDF, 236kB]