Critique of Mitscherlich's Law in Agronomy II
H. Schneeberger
Institute of Statistics, University of Erlangen-Nürnberg, Germany
2017, 23rd of November
Introduction
This paper is the continuation of paper [3], with the same title, there part I.
Meanwhile I got aware of the online version of a paper [5] with interesting data and with them I compared Mitscherlich's Law with my hypothesis in paper [3]. As I found great deficiences of Mitscherlich's Law, I decided to publish the results.
On this occasion it will be shown, that the method to compute the parameters of Mitscherlich's Law, given in [5], which is applicable only with essential restrictions to the data, is antiquated for a long time and that a much more general and simple (iterative nonlinear simplex-) method exists and is part, also for a long time, of program-packages, e.g. SAS.
Hypotheses and Data
Mitscherlich's hypothesis is, in the terminology of Schneider [5]
y = A(1-10-c(x+b)) (1)
(x=fertilizer, y=yield). To make this formula comparable with that of myself in [3]
(B)ŷ = a(1-e-b(x-d)) (2)
(y ist the experimental, ŷ the hypothetical value), I will mark Schneider's parameters by adding an S, because the meaning of the parameter b is different by both authors. Then a =As, 10-cs(x+bs)=e-b(x-d).
Because of 10α=e(ln10)α and ln10=2.30258 (=k), we get e-kcs(x+bs)= e-b(x-d)) and so
a=As; b=kcs; d= -bs; with k=2.30268(3)
The function (2) with a>0, b>0 is a growth-process with horizontal asymptote y=a. Mitscherlich called it "Gesetz vom abnehmenden Ertragszuwachs" (law of decreasing increase). That means : y'>0 and y''<0 for all positive values of x. x=0 is the beginning of extern fertilizing.
But it was already evident to Mitscherlich, that a horizontal final asymptote was not realistic; that the function y=yield must turn to a decrease and at last comes to zero: "In a salt-desert nothing can grow".
To consider this fact, I proposed in [3] the alternative hypothesis
(A) ŷ=a(x-d)2 e-b(x-d)(4)
I interprete this formula in the following way: Yield ŷ ist the superposition of two processes: A growing process (x-d)2, superposed (from the beginning x=d) by an exponential survival function e-b(x-d) , which is 1 at the beginning and goes exponentially to zero. Similar as in life.
Now the mathematical problem is the estimation of the parameters of (A) and (B) with an effective method. The mostly practised method is the method of least squares of Gauss, i.e. the parameters shall minimize the objective function
Q(a,b,d) = ∑(y-ŷ)2 (5)
Summation goes from 1 to n, the number of data.
Q is a nonlinear function of the parameters. If Q would be linear, the problem of minimization would be solved with the well-known set of normal r (linear) normal equations, where r is the number of parameters. Schneider tries this way also for the nonlinear function (B). To solve the system of 3 equations, which is now nonlinear in the unknown parameters, he must make the restriction, that the data-points are equidistant in x. That this procedure comes to a solution surely depends on the favourable function ŷ in (B). But in 1963, when Schneider's paper was published, no general methods to solve such problems existed; as far as I know.
Against that the author used for estimating the parameters a, b and d of (B) and of (A) the very effective method of Nelder & Mead [2] published 1965. There is no restriction to data and no partial differentiation of the objective function. I didn't use a commercial, but an own program for optimizing Q.
In table 1 the values of the experiment are given. x are the values of fertilizer N, y are the means of 4 values of yield (oats).
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| x | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 |
| y | 47.6 | 81.7 | 107.5 | 116.7 | 111.7 |
Results
A. Mitscherlich' s hypothesis
Schneider [5] with his method of computation and with his terminology for the parameters of formula (1) gets
As=119.60; bs=-0.146; cs=0.845(6)
and with these results the (optimal) value of Qopt=70.98, which ist he measure of coincidence of data-points and hypothesis.
In my terminology (see formula (2)) (6) becomes:
a=As=119.6; b=kcs=1.945; d=-bs=0.146(7a)
The computation with the method of Nelder & Mead (1965) resulted in the estimates
a=119.6; b=1.928; d=0.1438(7b)
and herewith
(B) ŷ=119.6(1-e-1.928(x-0.1438))(8)
and
Qopt=69.94
See figure 1, curve (B). So there is no essential difference in the two results (7a) and (7b).
For further discussion of Mitscherlichs hypothesis the parameters (7b) and formula (8)/curve B were used.
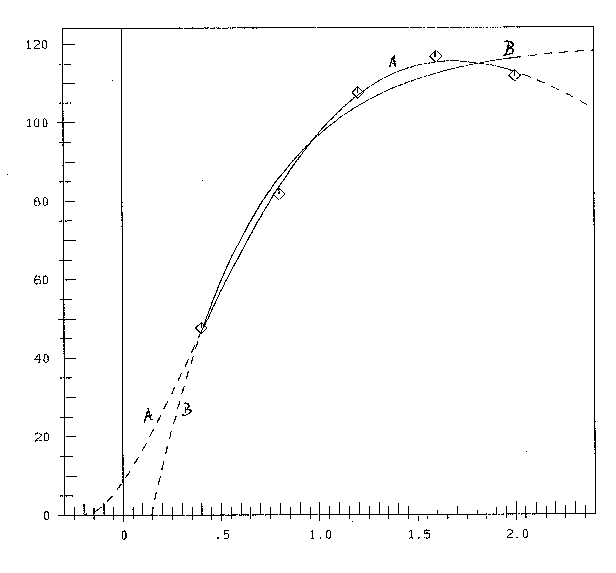
Fig.1: Mitscherlich's curve B: ŷ=a(1-e-b(x-d)); Alternative curve A: ŷ=a(x-d)2 e-b(x-d)
B. Alternative hypothesis
The computation of the parameters of formula (4) or for curve A of figure 1 with the method of Nelder & Mead (1965) resulted in the optimal parameters
a=237.1; b=1.054; d=-0,2127 (9)
and
(A) ŷ=237.1(x+0.2127)2 e-1.054(x+0.2127) (10)
with Q0pt=8.10.
You see, that the coincidence of data and hypothesis is much better for hypothesis (A) than for Mitscherlich's hypothesis (B). This is numerically shown by the ratio of the two optimal Q-values: 8.10/69.94 or 1/8.6. In figure 1 curve (A) is very near to all 5 data-points, and also turns down to point 5, as overfertilization has begun.
In his paper Schneider on page 78 states, that bs(=-d) can be seen as quantity of fertilizer in the soil before (extern) fertilization. In his computation bs=-0.146<0. That cannot be. Apriori negative quantity of fertilizer! According to figure 1, curve B, for x=d =+0.146 (bs=-0.146) yield is zero. For fertilization (from extern) with 0<x<-bs no yield would be. According to Mitscherlichs curve even a negative yield.
Against that hypothesis A: For x=0 (no extern fertilizing) yield is ŷ=8.57. This is the yield, which is brought by the soil-immanent fertilizer -d=0.2127. See figure 1, curve A.
The curve A has 4 regions of different character, as already shown in paper [3]. They are separated by extrema and points of inflection. Minima are at x=d=-0.2127 and for x=∞. A maximum is at xM=1.6848. Points of inflection are at xw1=0.3423 and xw2=3.0263.
In region I (d<x<xw1) we have increasing increase (y'>0 for increase of y, and y''>0 for increase of y')
In region II (xw1<x<xM) we have decreasing increase (y'>0; y''<0)
In region III (xM<x<xw2) we have increasing decrease (y'< 0; y''<0)
In region IV (xw2<x<∞) we have decreasing decrease (y'<0; y''>0)
Only region II is "Mitscherlich's region". Of the presented data only points 1,2,3 and 4 are included in this region. That point 5 doesn't belong to this family can be seen instantly in table1: y5<y4. Overfertilization is given. See also[4].
It is of interest, how well the coincidence of data and Mitscherlich's hypothesis is, when only data of region II are used for computation. The computation with data 1,..,4 and formula (2) resulted in
(C) ŷ=136.7(1-e-1.299(x-0.738))(11)
In figure 2 both Mitscherlich-curves (B) (with 5 data-points as computing basis) and (C) (with 4 data-points) are plotted. The coincidence of curve (C) and the first 4 data-points is now much better (Q=10.71) than it is for (B). But the asmptotic value of ŷ for (C) is 136.7, a far too high value. The maximum value of curve (A) is 115.53! So Mitscherlich's hypothesis may prognosticate a far too high yield, while there is already increasing overfertilization with decreasing yield and with its consequences in ecology.
An interesting detail: The measure of coincidence QOpt=8.10 for hypothesis (A) is still better=smaller than that for (C): 10.71, although for curve (C) only 4 points have to be approximated against 5 points for curve (A). A good omen for hypothesis (A).
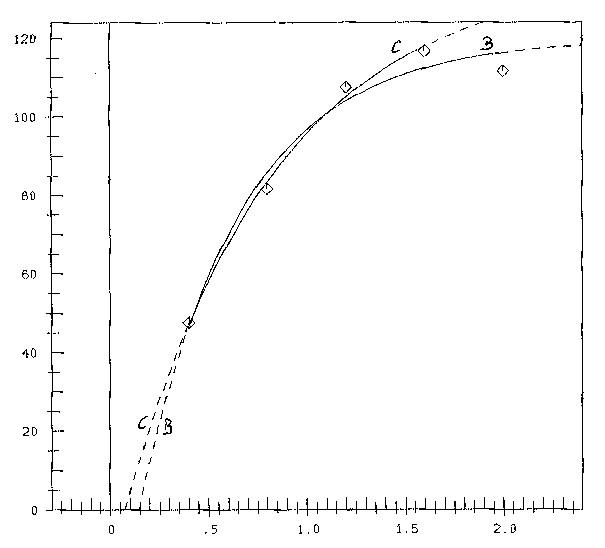
Fig.2: Mitscherlich's curves ŷ=a(1-e-b(x-d)); B: computed with all 5 data-points; C: computed with the first 4 "allowable" data-points
References
[1] Mitscherlich, E.A. (1909). Das Gesetz des Minimums und das Gesetz des abnehmenden Bodenertrags, Landwirtschaftliche Jahrbücher, 38, 537-553
[2] Nelder, J.R. and Mead, R. (1965). A Simplex Method for function minimization, The Computer Journal, 7, 303-313
[5] Schneider, B. (1963). Die Bestimmung der Parameter im Ertragsgesetz von E.A. Mitscherlich, Biometrische Zeitschrift, vol.5, issue 2, 78-95
Version of record online 23.Jan 2007
Download this paper as PDF
Download this Paper in PDF format:
Critique of Mitscherlich's Law in Agronomy II [PDF, 385 kB]