Over-Fertilization can be - and you do not notice it
H. Schneeberger
Institute of Statistics, University of Erlangen-Nürnberg, Germany
2012, 23th February
In a recent paper Kremper (Kremper R. et al., 2011) investigated the yield of dry-matter of ryegrass in dependence on the fertilizers N, P, and Zn. For Zn it was explicitly stated, that "the soil (meadow chernozem soil) was Zn-deficient". It will be shown, that the experimental results give another result: The soil is Zn-saturated to Zn-overfertilized. Perhaps the statement "Zn-deficience" results from former times - before extensive Zn-fertilizing.
15 treatments were made. Each treatment consisted of 4 pots (8 pots for treatment 15) with 2500 g of air-dry soil and the same quantity of fertilizers N, P and Zn (mg/kg). These quantities are given in Kremper's paper in table 1, the yields y (g/pot) are given there in table 2.
These results - with means ![]() instead of the individual 4 resp 8 ones of y - are repeated in table 1 of this paper. Because of the lower variance of the
instead of the individual 4 resp 8 ones of y - are repeated in table 1 of this paper. Because of the lower variance of the ![]() -values compared with that of the y-values, the points (fertilizer x;
-values compared with that of the y-values, the points (fertilizer x; ![]() ) better approximate the true (fertilizer=x, yield=y)-curve. This is a contribution to the good planning of the experiments.
) better approximate the true (fertilizer=x, yield=y)-curve. This is a contribution to the good planning of the experiments.
| number of treatment | N [mg/kg] |
P2O5 [mg/kg] |
Zn [mg/kg] |
mean of dry matter [g/pot] |
| 1 | 120 | 120 | 6 | 12.85 |
| 2 | 40 | 120 | 6 | 10.575 |
| 3 | 120 | 40 | 6 | 12.2 |
| 4 | 40 | 40 | 6 | 10.675 |
| 5 | 120 | 120 | 2 | 13.075 |
| 6 | 40 | 120 | 2 | 10.7 |
| 7 | 120 | 40 | 2 | 12.675 |
| 8 | 40 | 40 | 2 | 10.8 |
| 9 | 160 | 80 | 4 | 13.325 |
| 10 | 0 | 80 | 4 | 8.9 |
| 11 | 80 | 160 | 4 | 12.45 |
| 12 | 80 | 0 | 4 | 11.725 |
| 13 | 80 | 80 | 8 | 11.675 |
| 14 | 80 | 80 | 0 | 13.55 |
| 15 | 80 | 80 | 4 | 13.2625 |
Dependence of yield y on fertilizer Zn = x
To find the dependence of y on x alone, we must hold the quantities of fertilizers N and P constant and seek for (at least) two different treatments. The result is given in table 2 of this paper. We have 7 pairs of values (N, P2O5)=const. with two different treatments and get:
For a greater quantity of x=Zn the quantity of yield ![]() is smaller. This means, that we are on the declining branch of the (fertilizer, yield)-curve, i.e. in the region of overfertilization.
is smaller. This means, that we are on the declining branch of the (fertilizer, yield)-curve, i.e. in the region of overfertilization.
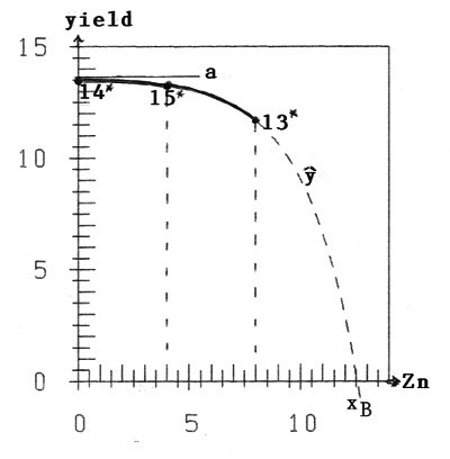
Still more interesting is the combination (N, P2O5) = (80; 80). Here we fortunately have three treatments and 14*, 15*, and 13* (14* means treatment 14) with different Zn-values.
| (N;P2O5) = const. | treatments | Zn [mg/kg] |
yield [g/pot] |
| (40;40) | 8 and 4 | 2<6 | 10.8 > 10.675 |
| (40;120) | 6 and 2 | 2<6 | 10.7 > 10.575 |
| (80;80) | 14 and 15 | 0<4 | 13.55 > 13.2625 |
| (80;80) | 15 and 13 | 4<8 | 13.2625 > 11.675 |
| (80;80) | 14 and 13 | 0<8 | 13.55 > 11.675 |
| (120;40) | 7 and 3 | 2<6 | 12.675 > 12.20 |
| (120;120) | 5 and 1 | 2<6 | 13.075 > 12.85 |
With the 16 experimental y-values of 14*, 15*, and 13* we can estimate the three parameters a, b, and xB of Schneeberger's hypothesis (Schneeberger, 2009b) of the declining branch of the fertilizer-yield-curve as an inverse Mitscherlich process:
ŷ = a(1-eb(x-xB)) (1)
We get a=13.61, b=0.427, xB=12.56; and herewith: ŷ(14*)=13.5, ŷ(15*)=13.2, ŷ(13*)=11.6
You can see in figure 1 the very good coincidence of the data-points (x, ŷ) with the points (x, ŷ) of the hypothetical curve (1).
The interpretation is: For data-point 14* we have x=0 (no fertilization): ŷ(x=0) = 13.5, approximately the asymptotic value a=13.61 of curve (1). The soil is Zn-saturated.
For data-point 15* we have fertilization with x=4: ŷ(x=4) = 13.2. So with Zn-fertilizing we get lower yield; the decrease is about 3%.
For data-point 13* with x=8 the decrease is already ca. 16%; and then with further fertilization it goes rapidly down with the yield.
 |
 |
| Figure 1: Yield as function of zinc Zn | Figure 2: Yield as function of nitrogen N |
We have three negative effects with Zn-fertilizing: Wasted money, decreased yield, poisoned soil.
Dependence of yield y on fertilizer N
Quite otherwise or normally is the case with fertilizer x=N as the only independent variable; (P,Zn)=const.
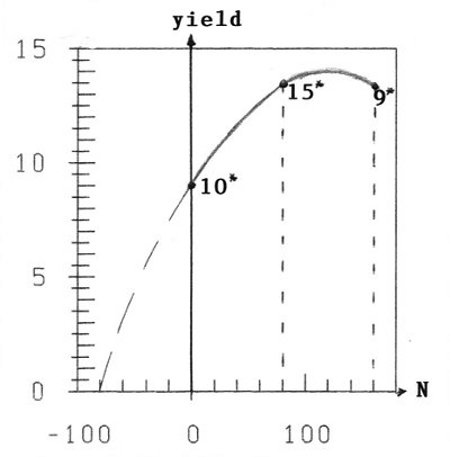
An analogous analysis for N as for Zn in table 2 yields: For all possible 7 combinations (P,Zn)=const. with two different N-values we get: For increasing x=N we get increasing yield ![]() .
.
For (P2O5,Zn)=(80,4) we fortunately have 3 different N-values with the treatments 10*(N=0,![]() =8.9; 15*(N=80,
=8.9; 15*(N=80,![]() =13.2625); 9*(N=160,
=13.2625); 9*(N=160,![]() =13.325.)
=13.325.)
As you see in figure 2, the maximum of the (fertilizer, yield)-curve lies between x=80 and x=160, i.e. treatment 9* lies already on the decreasing branch. Of course with one data-point on the decreasing part formula (1) cannot be applied, as well as Mitscherlich's formula with the 2 points on the increasing branch. So the curve of figure 2 is an approximate individual sketch.
Conclusion
It must be supposed, that there are many cases of fertilization, where the user means to be on the ascending branch of the (fertilizer, yield)-curve, and is already on the decreasing branch. And so his further fertilizing does not bring raising of the yield, but the contrary, combined with useless costs and poisoning of the soil. Is that for example a reason for the decreasing yields of maize after some years of intensive fertilizing? Some of my neighbours in upper-bavaria state this fact.
References
Kremper R. et al. (2011): Determination of Optimal Nitrogen, Phosphorus and Zinc Doses in a Multifactoral Pot Experiment. Communications in Soil Science and Plant Analysis, 42: 2229-2234
Schneeberger H. (2009b): Overfertilization: An inverse Mitscherlich Process: Internet: http://www.soil-statistic.de/overfertilization/overfertilization.html
Download this Paper in PDF format: Over-Fertilization can be - and you do not notice it (PDF, 0.7 MB)